Executive Summary:

The report presents a comprehensive literature review of dynamic ice-structure interaction models. The major models were discussed in details to identify their limitations and possible further development. Particular emphasis was given to ice induced vibration scenarios which is one of the most adverse outcome of dynamic ice loads. It was found that the current models do not include a number of ice parameters (for simplification) and hence are not able to simulate the complex ice-structure interaction behaviors such as continuous crushing or re-crystallization. So far, the reason for ice induced vibration is considered to be the self-excited oscillation due to the negative damping of the failure of the ice. However, the parameters influencing the failure of the ice i.e. negative damping is still unclear and hence the mechanism for ice induced vibration is not clearly understood yet.

By reviewing the papers, the above issues were identified which can be used as a guideline for proposing a new ice-structure interaction model. Moreover, the current computational methods for dynamic ice-structure interaction were also discussed in brief and their limitations in application of ice-structure interaction models were identified.

Table of Contents:

 

Executive Summary:

1 Introduction

1.1 Objective

1.2 Scope of the Project

2 Project Background

2.1 Historical Background

2.2 Overview of Ice-Structure Interaction

2.3 Genesis of Ice-Induced Vibration

3 Ice-Structure Interaction Models and Their Development

4 Incorporation of Ice-Induced Vibration

5 Computational Methods for Solving Ice-Structure Interaction Processes

6 Concluding Remarks

7 References

1           Introduction

Ice research has been facing new challenges everyday especially due to the hydrocarbon exploration in the Arctic and sub-arctic regions. Although the interaction between ice sheet and fixed structure is a fundamental phenomenon, a lot of question needs to be answered. It was earlier thought that dynamic ice-structure interaction is only important to cases where the structure is slender. However, the event of ‘molikpaq’ ¹ proved that any type of structure could get affected by such interactions. The most adverse outcome of dynamic ice-structure interaction is ice induced vibration and if not controlled properly this might lead to resonance. So far, a number of work has been done to formulate a model which would reflect such behaviors however due to the complex nature of the process most of them includes a number of assumptions. For further development, it is crucial that the key concepts of the current models are understood.

1.1         Objective

The project aims at reviewing the current analytical models developed for dynamic ice-structure interaction scenarios. Particular emphasis will be given on ice induced vibration scenarios which is the most adverse outcome of dynamic ice-structure interaction. Application of computational methods to solve the analytical models will also be discussed.

1.2         Scope of the Project

With a historical background of ice induced vibration, the report gives an overview of dynamic ice-structure interaction and ice induced vibration. Starting with the simplest ice-structure interaction model, the report introduces some of the key parameters for a more accurate ice load calculation. Ice induced vibration was highlighted from different researcher’s viewpoint to get a broader overview. A brief review of the computational methods to solve current ice-structure problem were also provided hence they are essential to solve the analytical models. Overall, the report will be a very good starting point for further development of dynamic ice-structure interaction model using numerical solution.

2         Project Background

2.1        Historical Background

When floating ice sheet moves against a fixed structure, the ice experiences increasing stress level until it reaches crushing. Since the grain boundaries are randomly oriented, the magnitude of the ice force will be somewhat random. Thus the prediction of ice load during such interaction becomes difficult to quantify. Also, when ice crushes against a compliant structure the contact force gradually increases when the structure resists movement against ice sheet. At this point, both ice and the structure are in elastic deformation and strain energy is stored with some of the energy being dissipated due to ice failure. At some point, when the crushing limit is reached, ice collapses. This causes a sudden decrease in the contact force and the structure swings back as the strain energy is released. The cycle starts again when the contact between the ice sheet and the structure is restored. The variation in the cyclic force results the structure to oscillate which is termed as Ice-Induced vibration (IIV). In some cases it may cause the structure to oscillate at one of its natural mode frequencies resulting in a frequency lock-in scenario. The frequency lock-in is a very dangerous phenomenon for the structure which is held responsible for the ‘molikpaq’ event mentioned above.

The adverse effect of ice induced vibration probably was first reported by Peyton ² for a vertical test pile erected in a temporary drilling platform in Cook Inlet, Alaska. In his report, he mentioned that the response of the structure is greatly dependent upon the velocity of the ice floe. At high velocities, the structure exhibits small amplitude, high frequency vibration whereas at low velocity, the amplitude undergoes severe, low-frequency variations between zero and a maximum level which is approximately double the high-velocity mean and is termed as “racheting”. According to Peyton, the structure receives most severe loading and acceleration when the floe is virtually stopped. Chinese oil production platforms at Bohai Sea were also damaged due to dynamic ice loads ³. In Finland, several resonant vibrations destroyed the superstructures of single steel piled lighthouses in 1973 ⁴. These incidents clearly indicated the need for more detailed study regarding dynamic ice-structure interaction.

2.2        Overview of Ice-Structure Interaction

When a plain level ice sheet approaches an engineering structure, the interaction depends on the structural geometry and physical properties of the ice as well as other boundary conditions such as velocity of interaction. At slow loading rate, the deformation of ice under stress might be modelled using viscoelastic theory however as the loading increases fracture and damage become prominent. The fracture process, ultimately leading to fragmentation governs the interaction concerning the far-field. In the near field, besides fracture, crushing and ice extrusion processes governs. Characteristic for crushing is the non-simultaneous contact at the interface between ice and structure ⁵ and most of the force is concentrated intensely in regions termed “high pressure zones.” The forces arising due to the interaction process above are generally considered being dependent on ice failure ⁶ and the force to fail the ice sheet determines the maximum load on the structure ⁷.

2.3        Genesis of Ice-Induced Vibration

To reduce the foundation cost, reduction of contact area is advantageous for structures that have to withstand moving ice loads. However, as the structure becomes slender it gets more prone to ice induced vibration. The vibration is typically generated by the moving ice cover during crushing when the crushing strength decreases rapidly beyond a certain point of strain rate. To illustrate this, the decrease of the strength may be interpreted as a negative damping element connected to the structure. When the positive damping element of the structure is greater than this negative damping the structure will be stable and no vibration will occur. Self-excited vibration will occur when this negative damping exceeds the positive damping of the structure. Based on his field measurement, Peyton² proposed that ice has a characteristic failure frequency of about one cycle per second. . Gaither ⁸ proposed that the failure oscillation is not a function of natural frequency of the structure but depends on ice thickness, temperature and loading rate. In his laboratory test he got constant frequencies for ice failures although he changed the natural frequency of the structure. Blenkarn ⁹ proposed that vibrations are due to the negative slope in ice crushing strength versus loading rate curve.

3         Ice-Structure Interaction Models and Their Development

The first model to predict ice structure interaction was probably proposed by Matlock et al ¹⁰. Considering the ice load at the cantilevered end of the structure, the model used a damped single degree-of-freedom oscillator system to represent the structure (Fig.1). The ice was replaced by a rigid base, on rollers transporting a series of elastic-brittle cantilever or teeth. The deformation of the tooth was proportional to the ice force unless it reaches a maximum value when fracture occurs and the tooth is permanently discarded. The interaction force remains zero until the next tooth comes into contact with the mass. The deformation of the tooth in contact was obtained from the relative displacement which was used to calculate the ice force.

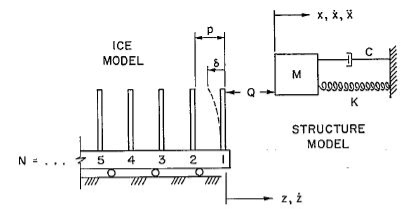
Figure 1: Mechanical analog of Ice-Structure Interaction ¹⁰

The differential equation of the motion was considered to be:

and N = Number of tooth in contact or next to be contacted

The interaction force is zero when

F=h.2∫0π/2σcσ,̇θcosθ adθ

Where

θ= polar angle,

σ̇= Stress rate.

As the velocity and properties of ice are kept constant vibration will occur only if the state of equilibrium is dynamically stable. For self-induced vibration, the stability can be divided into two groups: orbital stability at the origin and stable limit cycles. In the first case no vibration will occur and in the second case vibration will occur but amplitudes will grow finitely and after a while reach a steady state resulting a limit cycle. To find out the stability exact root extraction method, numerical integration method and simple approximative method were used as the general methods such as (Routh-Hourwitz, Liapunov etc.) does not give information about which natural mode shows stability or instability. The root extraction method was succeeded with QR-algorithm using “IMSL” subroutines. In case of stability, the equation of motion was first linearized and then transformed to a group of first order differential equations. The ice force was divided into two parts: the static component due to crushing strength with the initial constant ice velocity and to the change of relative velocity dependent component. The numerical integration was done by fourth order Range-Kutta scheme with a small initial disturbance. The principal mode presentation in numerical integration makes it possible to take into account only those modes which have significant effect on ice-structure interaction. An approximative stability requirement was calculated by following a perturbation method in which only the first approximation was considered. The authors were able to formulate a relationship in which the criteria for dynamic stability were expressed as simple engineering terms.

Huang and Liu ²⁶ modified Matlock’s model to develop a discrete failure type of dynamic model incorporating more properties of ice crushing such as velocity effect and stochastic characteristics. Based on the velocity of the mass and velocity of the ice cover, the equation of motion was modified for three separate conditions. The equation of motion and the displacement of the mass were then normalized and the equation for displacement was formulated for loading, extrusion and separation phase and solution was obtained. It was found that as the amplitude of vibration increases gradually, ice failure events occur when the structure and ice move in the same direction with the structure gaining momentum from the ice. In contrast, as the amplitude of vibration decreases gradually, ice failure events occur when the structure and ice move in an opposing direction with the ice gaining momentum from the structure. This is the typical feature of the resonant vibration, as observed by Engelbrektson ²⁷ in the Gulf of Bothnia. Further computation showed that this feature is dominant when the ratio between ice cover velocity and transitional ice relative velocity was between over 2.2 and 2.75.

Based on their outcome Huang and Liu ²⁶ discussed the ice velocity effect on mechanism of IIV. The ice-structure interaction plays dual roles in IIV, promoting and restraining the vibration of structures. However, the relative domination of the two roles is uneven for compliant structures, even if the velocity effect on the ice failure force is not involved. Due to the movement of the structure, the relative ice velocity is smaller when the structure and ice move in the same direction than in the opposing direction. Thus, the buffering action takes effect in the former case to lengthen the duration of ice-structure interaction before ice failure occurs and so the transmission of momentum or energy from ice to the structure is more than the inverse transmission in the latter case. This unevenness causes a net gain of energy for the structure, which is balanced by the damping dissipation and the potential and dynamic energies of the vibration in the steady vibration state. The velocity effect on the ice failure force further signifies the unevenness since not only the loading phase lengthens but also the ice force during the interaction increases when the ice and structure moves in the same direction. Consequently, the rate of the net energy gain increases so that the system stays in the dynamic equilibrium with higher amplitude of response. The resonant frequency lock-in maximized the net gain rate of energy. In addition, it was noted that a higher rate of net energy gain is produced when the ice velocity falls into such a range that the relative ice velocity remains in the descending portion of the ductile-brittle transition region, irrespective of the movement direction of the structure. This is because the alternation of the ice failure force is most remarkable in this range.

Shih ²⁸ used mathematical modelling technique to interpret some significant experimental observations on the ice-induced vibration for flexible structures. Harmonic components involved in the structural responses were identified first and a procedure to simulate the transient response was proposed with a graphic illustration.   Damping effects on the predominant frequency of structural response were also investigated with asset of analytical equation. It was found that the predominant frequency increases with the ice velocity up to a certain limit below the natural frequency of the responding structure. This predominant frequency is then locked in at a finite ice velocity.

5         Computational Methods for Solving Ice-Structure Interaction Processes

Computational methods are very useful for solving complex interaction process hence researchers have implied computational methods for ice-structure interaction problems over the last few decades.  Different approaches for numerical modelling exist and frequently two fundamentally different simulation techniques are consulted to solve the general boundary value problem:

• Continuum methods, such as the Finite Element Method (FEM), Finite Difference Method (FDM) and also Paricle-in-Cell (PIC) method
• Particle Methods, such as the Discrete Element Method (DEM)

The first attempts in utilizing computational methods for the ice indentation problem were probably done by Ralston ²⁹ and Reinick ³⁰ both of whom utilized plastic limit analysis, building upon an elasto-plastic response of the ice. They used unconfined ice strength values to define the yield function coefficients. Later, some of the researchers used finite element method (FEM) to solve ice sheet impact on different types of structures.

Sand and Horrigmoe ³¹ used non-linear finite element analysis to simulate ice forces on sloping structure. The ice was treated as an isotropic material capable of cracking and crushing. It was done by using a combination of Willam-Warnke’s failure criterion in compression and a maximum principle stress criterion in tension. Contact interaction forces were simulated with a contact algorithm that permits surface-to-surface contact with Coulomb friction and sliding. An iterative procedure for automatic calculation of the buoyancy force was also developed. It was found that the proposed iterative procedure for automatic calculation of the buoyancy forces is an effective method to establish buoyancy forces on a partially submerged body specially when the geometry of the partially submerged body becomes complex (in case of first year or multi-year ridges). For a number of friction co-efficients between ice and structure and sloping angles, numerical results of the horizontal ice force on a sloping structure were compared with analytical solutions and the deviation was small in general. However, when the slope angle becomes steep and the friction co-efficient large, the calculated force was much smaller than the one obtained from analytical solution. The authors believed this was due to the local crushing of ice in the vicinity of the structure which was not included in the analytical solution.

Derradji-Aouat ³² gave a brief summary for the constitutive model, damage formulation, failure criterion and numerical simulation for ice. He presented two examples with ice having both micro and macro cracks in ice-structure problems. The 1^st example was a numerical simulation of an ice sheet (100 by 60 by 0.5m) impacting a large fixed concrete structure (120 by 40 by 40 m) in the Bell Isle Strait (BIS), Newfoundland, Canada. The 2nd second example was a simulation of a cylindrical rigid indentor impacting an ice block (10 by 2 by 2 m) at high speed. Based on the outcome, he concluded that a constitutive model for ice (that includes damage, micro-cracking formulation), a failure criteria (that deals with large fracture in the ice media) and a robust numerical solution method (such as EFEM) can be all combined to produce a powerful tool that can be used to simulate the interactions of ice with actual offshore structures, and subsequently, calculate both local and global ice loads.

Martonen et al. ³³ used ANSYS structural commercial code for non-linear finite element simulation of indentation loads caused by an ice sheet on a rigid conical structure. The ice sheet was 20m × 20m and the structure was modeled as a 10m waterline diameter cone. The interaction between the structure and the ice sheet were modeled using a nonlinear 3-D contact element formulation. The mechanical behaviour of ice (constitutive model for ice) is elastic, while its failure was modeled using a multi surface failure criterion. The failure criterion included the effects of the strain (loading) rate, temperature, salinity and porosity on the magnitude of ice strength. During the simulations, failed elements (i.e. elements that satisfy the stress conditions of failure criterion) were taken out from the initial geometry of the ice sheet. Therefore, the process and sequence for breaking ice pieces from the original ice sheet were modeled. This was achieved via developing an ANSYS macro (routine) for element death numerical technique. The model was validated by comparing the computed ice loads from the numerical simulations with full-scale ice load measurements obtained from the Kemi-I test cone ³⁴.

Finite Difference method also received attention for solving ice-structure interaction problems. Matskevitch and Shikhinek ³⁵ considered the interaction between a pile and the frozen ice sheet around it. The ice sheet was moved against the structure in the horizontal plane by various external load factors. The problem was treated as a dynamic plane stress problem and an explicit finite difference method was used in the FORTRAN program SHELF-M to investigate the ice structure interaction. It was found that all parameters of yield function essentially affect the value of normalized effective ice pressure. Moslet ³⁶ used a two-dimensional finite difference program to simulate the stress state in the ice during interaction, rather than the ice force for his medium scale ice-structure interaction test. The results show that the tensile tangential stress that occurs as a result of the shape of the structure is an important factor in limiting the force exerted by the ice. Barker et al. ³⁷ on the on the other hand, used the PIC method to simulate ice loads on a bridge pier. In the PIC method the ice volume is partitioned into individual particles and their motion is integrated in a Lagrangian sense. The particle ice volume is interpolated onto a fixed Eulerian grid on which the momentum equations are solved to obtain particle velocities. The method follows continuum rheology with constitutive properties being smeared out. The PIC method tracks the densities within a grid projected onto the computational problem. Ice accumulation may thereby be simulated, whereas, due to the continuum assumption, mathematical discontinuity cannot be accounted for.

The latest addition to the computational methods to solve ice-structure problem is the Discrete Element Method (DEM). Instead of using continuum mechanics (like FEM) discrete elements generates the model made of consisting of a number of particles bonded together (like molecular dynamics). This facilitates the simulation of ice behavior in the granular level specially during crushing. Jirasek and Bazant ³⁸ proposed a particle model for quasibrittle fracture which can be applied to sea ice. The particles at the micro level were modeled to interact only by the central force with a prescribed force-displacement or stress-strain relations which exhibits postpeak softening and was characterized by microstrength and microfracture energy. Unlike the regular lattice structure used in continuum mechanics, a randomly generated particle model has no biasness. It was proposed that, with a proper choice of the microlevel constitutive law, it can realistically simulate fracture of an ice floe during impact on a rigid obstacle.

Slevdurai and Sepehr ³⁹ performed a two-dimensional discrete element method for the study of the plane strain problem of the interaction between a moving ice sheet and a flexible stationary structure. Two aspects were investigated which included the utilization of the same failure criteria for describing both the initiation of viscoplastic flow in compression range and fragmentation in the tensile range and the inclusion of size dependency in the strength characteristics of the fragments that are produced during the interaction process. The first modification was incorporated to support the experimental observations which suggested that the processes of brittle fragmentation would occur in regions where the stress state is predominantly tensile and viscoplastic flow would occur in regions where the state of stress is predominantly compressive. The second modification was incorporated to limit the size of fragments developed during the interaction process which significantly influences the computational efficiency and the stability of the solution process. The modified discrete element code was applied to examine the dynamic interaction between an ice sheet of constant thickness moving at a uniform speed with a stationary flexible structure.

The first problem considered an interacting ice sheet where a leading region of the ice sheet possesses initial elastic characteristics and brittle fragmentation behaviour both in tension and compression. The remaining length was modelled as a non-fragmentable elastic layer. The fragmentation process observed was found to duplicate the realistic fragmentation process limited only by a strength dependent fragment of size with a lowest edge length of 0.2m. The time-dependent evolution of average contact stress exhibited the characteristic ‘load accumulation-load shedding’ feature observed during many ice structure interaction phenomena. The second problem examined was similar in character except that only the leading ice sheet was modelled by a fragmentable, viscoplastic material. Similar type of ‘load accumulation-load shedding’ feature was observed in the time dependent evolution of average contact stress. Higher average contact stresses were, however, observed for this example as the ice sheet behaved as a region which can sustain stresses without shedding such loads by a fragmentation process.

Lau ⁴⁰ performed a series of discrete element analysis of ice sheet interaction with a 60⁰ conical bridge pier. Six runs were conducted using a three dimensional discreet element program “DECICE3D.” The code was based upon a dynamic equilibrium explicit time stepping formulation and centers around a sophisticated housekeeping logic. The logic was specially designed to track the behavior and response of a large number of deformable bodies efficiently. The bodies were permitted to be in contact with each other undergoing large non-linear deformation and discrete featuring. Although the model test data for the force calculation showed good agreement with field measurement, major discrepancy was found in the formation of subsidiary cracks and the subsequent rubble pileup.

6         Concluding Remarks

Most of the arctic projects include a dynamic load factor for the design purposes based on the previous data. However as we are expecting exploration further north, the existing data might not be good enough for calculating dynamic ice load. To avoid over or under estimate, a good understanding of the ice-structure interaction and a dynamic ice load model is very important.

The current models still lacks a proper ice load models and are based on a number of assumptions for ice parameters. Moreover, loads due to the crushing failure still lacks proper understanding and the current models are unable to find the ice loads for such type of failure. Crushing failure is also considered to be responsible for triggering ice induced vibration which as discussed earlier could lead to resonance if synchronized with the natural frequency of the structure. Identifying the behavior of high pressure zones (hpz) might be an answer of the problems as most of the forces get transmitted through such small areas. If their behavior could be modelled properly, they might be able to simulate the crushing failure. A dynamic model incorporating high pressure zones (hpz) could probably reflect the dynamic ice loads as well as criteria for triggering ice induced vibration.

Finally, as discussed earlier, conventional finite element method is not enough for numerical simulation of ice-structure interaction as the failure is unpredictable for ice and it involves a number of complex processes. So far, discreet element method seems promising but still lacks the capability of simulating continuous crushing and recrystalization. Much work is needed in both these areas to propose an ultimate dynamic ice-structure model which can be used for universal conditions.

1. Jefferies MG, Wright WH. Dynamic response of ‘molikpaq’ to ice structure interaction. . 1988;4:201-220.

2. Peyton H. Sea ice forces. ice pressure against structures. Technical Memorandum. 1968(92):117-123.

3. Wang K, Wu H, Wang C, Liu L. Modelling sea ice ride-up and pile-up against conical caisson in bohai bay. . 1998:939-945.

4. Maattanen M. Experience of ice forces against a steel lighthouse mounted on the seabed and proposed constructional refinement. . 1975.

5. Jordaan IJ. Mechanics of ice-structure interaction. Eng Fract Mech. 2001;68(17-18):1923-1960. http://dx.doi.org/10.1016/S0013-7944(01)00032-7. doi: 10.1016/S0013-7944(01)00032-7.

6. Fransson L, Olofsson T, Sandkvist J. Observations of the failure process in ice blocks crushed by a flat indentor. . 1991;1:501-514.

7. Sodhi DS, Haehnel RB. Crushing ice forces on structures. J Cold Regions Eng. 2003;17(4):153-170. http://dx.doi.org/10.1061/(ASCE)0887-381X(2003)17:4(153). doi: 10.1061/(ASCE)0887-381X(2003)17:4(153).

8. Gaither WS. Ice forces on marine structures. . 1970.

9. Blenkarn KA. Measurement and analysis of ice forces on cook inlet structures. . 1970. doi: 10.4043/1261-MS.

10. Matlock H, Dawkins W,P., Panak J,J. A model for the prediction of ice-structure interaction. . 1969:687-694.

11. Kärnä T, Kamesaki K, Tsukuda H. A numerical model for dynamic ice–structure interaction. Comput Struct. 1999;72(4–5):645-658. doi: http://dx.doi.org/10.1016/S0045-7949(98)00337-X.

12. Eranti E. General theory of dynamic ice structure interaction with applications. . 1991:489-498.

13. Kry PR. Third canadian geotechnical colloquium: Ice forces on wide structures. Can Geotech J. 1980;17(1):97-113. http://dx.doi.org/10.1139/t80-009. doi: 10.1139/t80-009.

14. Withalm M, Hoffmann NP. Simulation of full-scale ice–structure-interaction by an extended matlock-model. Cold Reg Sci Technol. 2010;60(2):130-136. doi: http://dx.doi.org/10.1016/j.coldregions.2009.09.006.

15. Ashby M, Palmer A, Thouless M, Ponter A. Nonsimultaneous failure and ice loads on arct. . 1986.

16. Konuk I, Gürtner A, Yu S. A cohesive element framework for dynamic ice-structure interaction Problems—Part I: Review and formulation. . 2009:33-41.

17. Brown TG, Morsy UA. Modelling of continuous crushing of ice in front of offshore structures. Canadian Journal of Civil Engineering. 1995;22(3):544-550. http://dx.doi.org/10.1139/l95-063. doi: 10.1139/l95-063.

18. Frederking R. Ice pressure variations during indentation. . 2004;2:307-314.

19. Taylor R, S., Frederking RF, Jordaan I,J. The nature of high pressure zones in compressive ice failure. . 2008.

20. Taylor RS, Richard M. Development of a probabilistic ice load model based on empirical descriptions of high pressure zone attributes. . 2014;10:Ocean, Offshore and Arctic Engineering Division. http://dx.doi.org/10.1115/OMAE2014-24353. doi: 10.1115/OMAE2014-24353.

21. Richard M, Taylor RS. Analysis of high pressure zone attributes from tactile pressure sensor field data. . 2014;10:Ocean, Offshore and Arctic Engineering Division. http://dx.doi.org/10.1115/OMAE2014-24342. doi: 10.1115/OMAE2014-24342.

22. Määttänen M. On conditions for the rise of self-excited ice-induced autonomous oscillations in slender marine pile structures. . 1978;25:98.

23. Hirayama K, Schwarz J, Wu H, IOWA INST OF HYDRAULIC RESEARCH IOWA CITY. An investigation of ice forces on vertical structures. . 1974. www.summon.com.

24. Michel B, Toussain N. Mechanisms and theory of indentation of ice plates. . 1976.

25. Timoshenko S, Young DH, Weaver W. Vibration problems in engineering. . 1974. www.summon.com.

26. Huang G, Liu P. A dynamic model for ice-induced vibration of structures. Journal of Offshore Mechanics and Arctic Engineering. 2009;131(1):1-6. http://dx.doi.org/10.1115/1.2979795. doi: 10.1115/1.2979795.

27. Engelbrektson A. OBSERVATIONS OF A RESONANCE VIBRATING LIGHTHOUSE STRUCTURE IN MOVING ICE. In: Vol 28. ; 1983:855-864.

28. Shih LY. Analysis of ice-induced vibrations on a flexible structure. Appl Math Model. 1991;15(11–12):632-638. doi: http://dx.doi.org/10.1016/S0307-904X(09)81009-3.

29. Ralston TD. Yield and plastic deformation in ice crushing failure. ; 1980.

30. Reinicke K. Analytical approach for the determination of ice forces using plasticity theory. In: Physics and mechanics of ice. Springer; 1980:325-341.

31. Sand B, Horrigmoe G. Simulation of ice forces on sloping structures. ; 1998:476-482.

32. Derradji-Aouat A. Explicit fea and constitutive modelling of damage and fracture in polycrystalline ice – simulations of ice loads on offshore structures. Proceedings of the International Conference on Port and Ocean Engineering under Arctic Conditions, POAC. 2005:225-238.

33. Martonen P, Derradji-Aouat A, Määttänen M, Surkov G. Non-linear finite elements simulations of level ice forces on offshore structures using a multi surface failure criterion. . 2003:223-232.

34. Määttänen M, Nortala-Hoikkanen A, Avis J. Ice failure and ice loads on a conical structure – kemi-I cone full-scale ice force measurement data analysis. . 1996;1:8-16.

35. Matskevitch D, Shkhinek K. A computer-based simulation of the ice fracture near a vertical pile. Int J Offshore Polar Eng. 1992;2(2):123-128.

36. Moslet PO. Medium scale ice–structure interaction. Cold Reg Sci Technol. 2008;54(2):143-152. doi: 10.1016/j.coldregions.2008.03.001.

37. Barker A, Sayed M, Timco GW. Numerical simulation of floating ice forces on bridge piers. In: ; 2000:76.

38. Ba ant ZkP, Jirásek M. Particle model for quasibrittle fracture and application to sea ice. J Eng Mech. 1995;121(9):1016-1025. doi: 10.1061/(ASCE)0733-9399(1995)121:9(1016).

39. Selvadurai APS, Sepehr K. Two-dimensional discrete element simulations of ice – structure interaction. Int J Solids Structures. 1999;36(31-32):4919-4940.

40. Lau M. Three dimensional discrete element simulation of ice sheet impacting a 60-degree conical structure. . 2001.